Как решать задачи?

Хороший вопрос, верно?

Очень хочется знать ответ … Должна же быть какая-то тайна, недостающее звено, утерянное школьным образованием, из-за отсутствия которого распадается на куски полотно понимания! И не только математики, но и понимания вообще. И главная болезнь школьного образования — «наличие этого отсутствия».

… В статье я покажу на простом примере :

• чему можно научиться, решая простейшие задачи;
• как работает ум при решении задач и
• почему решать задачи действительно трудно.
• А также, почему школа решать задачи не учит.

Совсем.

Да, метод решения задач существует. Но в школе он

не применяется. Фактически он под запретом. Большинство школьников потеряли способность разбираться с решением задач настолько, что не улавливают правильное направление, даже когда его показываешь.

Как я решаю школьные задачи (пример)

И как я решал их, когда был школьником. Это было давно, но я все помню … Видимо, потому, что учился решать задачи, а не запоминать «типовые решения определенного класса задач».

Вот задача:

«Одну сторону прямоугольника увеличили на 25%. Как нужно изменить другую сторону, чтобы площадь осталась прежней?»

Откуда эта задача я забыл. Но помню, что сын, решая ее в третьем классе, неожиданно «притормозил».

… Чтобы уловить причину затруднения при решении такой простой задачи нужно уметь решать самому, а не просто «знать ход решения». Это намек на учителей. Большинство из них не понимают, где здесь можно запутаться и сразу начинают орать: «Такие задачи мы уже решали» и «Ты должен знать» и прочую хрень. Потому, что никогда в своей жизни задач по математике не решали. Только «проходили решение задач этого типа».

Поскольку я не учитель, то увидеть «ровное место», на котором споткнулся сын, мне было нетрудно.

Вот реконструкция мыслей думающего человека при решении подобных задач.

Почему сложно решать текстовые задачи

«Понять условие – значит решить задачу». Известная мудрость.

Где в условии задачи подвох?

«У прямоугольника 2 стороны: большая и меньшая. Площадь прямоугольника равна произведению … и т.п.». Так «решают» задачи учителя.

Но третьекласснику показалось, что сторон у четырехугольника больше двух. Аж четыре!.. Поэтому представив условие он «притормозил»: «Какую именно другую сторону следует уменьшить?..»

Взрослому трудно понять такого рода трудности. Большинство «знает», что у прямоугольника две стороны: А и В. Поэтому большинство взрослых не способно к творчеству.

И большинство взрослых не умеют учить.

А дети пока умеют: и учиться и творить…

Решение задачи школьным методом

Решение несложное. Нужно знать, как вычислить площадь прямоугольника.

Если один из сомножителей умножить на 1,25 (то есть увеличить на 25%), то для сохранения произведения нужно другой сомножитель разделить на 1,25.

Несложно.

Хотя я рекомендовал бы расписать все на бумажке.

Зачем? Давайте смотреть дальше…

Обязательно ли четырехугольник после увеличения «одной из сторон» останется прямоугольным?

И если нет, то:

• окажется ли площадь произвольного четырехугольника равна площади исходного прямоугольника?

«Узри, чтобы понять!»,

— воскликнул арабский, кажется, математик, обнаружив еще одно доказательство теоремы Пифагора. Не «Посчитай» …

Я простой смертный и могу ошибаться. Мое отличие от большинства других смертных в том, что зная это, я не полагаюсь на «абстрактный» ум, забитый «типовыми решениями».

… Давайте изобразим частный случай трансформации прямоугольника после увеличения «одной из сторон» на 25%.

Менее очевидное, но не менее шаблонное решение

Пользователь оставил комментарий к моему видео «Как понимать математику (абстрактное и конкретное мышление)».

«Задача, как ее понял ваш сын, также решается просто: другую сторону прямоугольника нужно уменьшить на 25%».

Я ответил:

«Неверно. Площадь произвольного четырехугольника не будет равна площади исходного прямоугольника. И видео это не о том, как считать, а о том, как понять, что именно нужно считать».

Честно говоря, я попался ….

… Но знание того, что люди склонны ошибаться, а я — человек, помогает выбираться из ловушек очевидности. Даже если в них попадаешься …

Может ли быть более одного правильного решения задачи?

Почувствовав неладное, я нарисовал картинку:

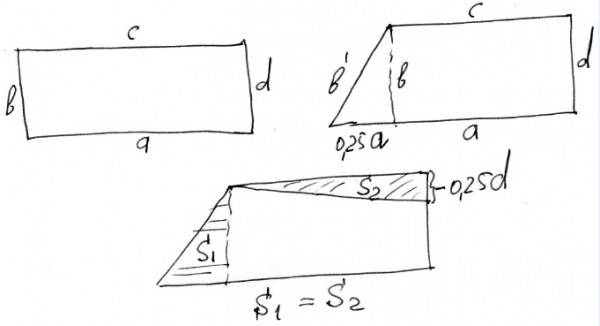
И … понял, что комментатор прав.

Можно алгебраически показать, что площади двух заштрихованных треугольников равны. Следовательно, площадь получившегося четырехугольника также равна площади исходного прямоугольника …

Здесь «Правое» встречается с «Левым». (Декарт, кажется, впервые ввел в алгебру геометрию, придумав систему координат.)

Эта задачка — пример, в котором весьма затруднительно доказать равенство чисто геометрически. Алгебраически же … А что именно тогда считать, не изобразив условие?..)

Чувство правильного решения

Некоторое чувство, инстинкт понимания, которые развиваются в процессе решения задач, шептали мне: что-то здесь не сходится …

… Наш мозг так устроен, что экономит энергию буквально на всем. А очевидное — это привычное, шаблонное, легкое. Поэтому мозг всегда толкает нас в сторону известного и привычного …

Комментатор (нужно отдать ему должное) внимательно смотрел видео и решил задачу менее стандартно. Но … действовал по той же схеме «энергосбережения».

Шаблоны бывают разного уровня, но шаблон есть шаблон. Всегда найдется задача, на которой он не сработает и привычное решение окажется неверным …

(На это, замечу и рассчитана ловушка ЕГЭ: учить запоминать, а потом давать задачи на понимание).

Еще менее очевидное решение задачи …

«У прямоугольника 4 стороны. И если одну из них увеличили на 25%, то почему он взял именно эту, «удобную» сторону?»,- подумал я. Как, видимо, подумал и мой сын, который не смог оформить эту мысль, поэтому просто «притормозил».

Почему не взять другую сторону b? Ту, что изменилась при увеличении стороны a? Ведь говорится просто о «другой» стороне?

Да потому, что ум нашептывает: этот вариант посчитать будет труднее!

В предыдущих двух примерах решение получалось:

• В первом случае, по формуле площади прямоугольника мы просто умножали и делили.
• Во втором случае, чтобы узнать что на что умножать, нам пришлось изобразить задачу, а потом, посчитав площади двух заштрихованных треугольников, увидеть, что они равны.

В третьем же случае …

… Изобразим условие задачи и узрим ответ.

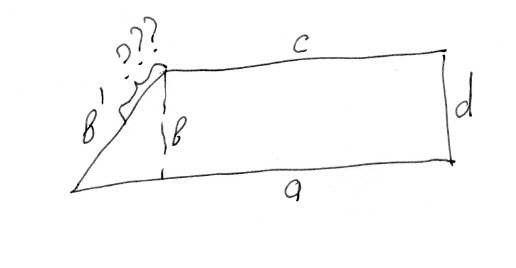
Что получится, если после увеличения на 25% стороны a уменьшить на 25% сторону b, а не удобную для решения сторону d? Что будет, если мы уменьшим на 25% сторону, только что ставшую функцией изменения другой стороны?

… Сравнить площади возникшего неправильного и исходного правильного четырехугольников с использованием только Пифагоровой теоремы не получится.

И совсем не очевидно, что

• площади получившегося четырехугольника и
• исходного прямоугольника

равны …

---

Если бы мы не изобразили задачу, не поигрались с рисунком, то не подобрались бы к более глубокому пониманию … Не решили бы задачу.

И вот правильное направление в обучении.

• Чтобы научиться решать задачи, нужно выработать привычку всматриваться в условие. Так можно научиться думать и перестать бояться экзаменов.

Равно, как и школьных учителей, абсолютное большинство которых думать и решать задачи не умеет. И не может этому научить.

---

…Откуда возникает чувство, которое подсказывает: что-то здесь не складывается … Давай взглянем еще раз…

Решение задач, имеющих практический смысл (источник понимания)

Поскольку мне пришлось довольно плотно заниматься финансовыми инструментами, то я вынужден был научиться чувствовать некоторые фокусы, связанные с процентами. От этого зависело выживание моего депозита.

Просто взглянув на задачу о прямоугольнике, можно почувствовать: что-то здесь не так.

Попробуйте доказать (или опровергнуть) утверждение:

И если вы это сделаете, то поймете:

• почему можно «притормозить», размышляя над этой задачей.
• Что эту задачу невозможно решить на уровне 3, 4, 5 классов.
• Что ответ «Верно» или «Нет» зависит от выбранной модели решения. (И здесь их минимум три).

И еще вы заметите, что на «простой» задаче можно научить ребенка думать и решать очень широкий класс задач … Если учить именно решать и думать, а не умножать «ширину на высоту».

---

Да, иногда чувства обманывают.

Но иногда они же подсказывают направление, в котором есть смысл двигаться и, возможно, что-то найти. В этом мире нет точных шаблонов на все случаи, но есть направления, двигаясь по которым чаще находишь что-то полезное. И становишься умнее, способнее, успешнее. Иногда даже счастливее …

---

На закуску еще одна

действительно простая задачка.

Решите ее быстро, как это требуют в школе.

Величину А увеличили на 100%. На сколько процентов нужно уменьшить результат, чтобы вернуться в «исходное состояние»?

По опыту: менее одного человека из ста правильно решают подобные задачи. А ведь стоит нарисовать это, как получить неправильный ответ становится сложно!

Вот и думайте:

• разрешать ли ребенку пользоваться счетными палочками, пальцами, счетами,
• провоцировать изображать условие задачи на бумаге или
• слушать школьных авторитетов, авторов современной школьной методики обучения, которые в решении задач не понимают ни хрена …

---

P.S.

Меня уже успели спросить: а при чем тут проценты и эта задача?

Это третья модель решения

По условию одну сторону (допустим ширину) увеличили на четверть. Получился прямоугольник, площадь которого увеличилась на четверть.

На сколько нужно изменить «другую сторону» …

Ваше решение?

Запись только для зарегистрированных